Boron Nitride sheet as a novel surface for medical adsorption and drug synthesis

Introduction

Boron nitride is a synthetic material, which although discovered in the early 19^th century was not developed as a commercial material until the latter half of the 20^th century. Boron and nitrogen are neighbors of carbon in the periodic table – in combination boron and nitrogen have the same number of outer shell electrons – the atomic radii of boron and nitrogen are similar to that of carbon. It is not surprising therefore that boron nitride and carbon exhibit similarity in their crystal structure (1-5).In the same way that carbon exists as graphite and diamond, boron nitride can be synthesized in hexagonal and cubic forms.  Hexagonal boron nitride (h-BN) is the equivalent in structure of graphite. Like graphite its plate like microstructure and layered lattice structure give it good lubricating properties. h-BN is resistant to sintering and is usually formed by hot pressing (6-10). BN is a very good electrical insulator. It offers very high thermal conductivity and good thermal shock resistance.

Unlike graphene, a h-BN sheet is a wide gap insulator, as is bulk h-BN, and is a promising material for opto-electronic technologies, tunnel devices and field-effect transistors. Using a combination of mechanical exfoliation and reactive ion etching, monolayer and multilayer suspended h-BN sheets can be prepared. The band gap of boron nitride nanoribbons can be altered by edge passivation with different types of atoms. A combination of an odd number of h-BN layers is a non-centrosymmetric ionic crystal which is piezoelectric due to D3h symmetry. The corrugations on the h-BN sheet results in a strong polarization in the plane of the sheet which depends non-analytically on the wave vector of the corrugations.  h-BN sheet has a non-linear elastic deformation up to an ultimate strength followed by a strain softening to failure. Moreover, the band gap of boron nitride nanotubes can be reduced by a transverse electric field due to a mixing of states within the highest occupied molecular orbital and the lowest unoccupied molecular orbital. The reduction in the band gap due to uniaxial strain results in tunneling magnetoresistance ratio which increases linearly with applied strain(11-15).

Boron nitride (BN) is a modern man made compound that perfectly parallels the crystalline structure and properties of naturally occurring elementary carbon. Actually hexagonal boron nitride hBN (or white graphite) is a high performance lubricant similar to natural graphite, while cubic boron nitride cBN (or borazone) is second in hardness after diamond, both substances being classified as the best superabrasives. Even more, a perfect crystallographic analogy exists between the boron nitride polymorphs and the carbon allotropes: hBN (hexagonal boron nitride) has the same crystal lattice as graphite, rBN (rhombohedral boron nitride) has the same crystal lattice as rhombohedral graphite, cBN (cubic boron nitride) has the same crystal lattice as diamond, wBN (wurtzitic boron nitride) has the same crystal lattice as lonsdaleite (a wurtzitic variety of diamond). For boron nitride as well as for carbon the same distinction can be made between the low density –low hardness polymorphs and high density – high hardness polymorphs (16).

Boron nitride has a great potential in nanotechnology. The studies show that BN may be particularly suitable for biological applications.The objective of the present work was to investigate the adsorption potential of Boron Nitride (17-24).

The two pairs of nucleobases, adenine (A) with thymine (T) and cytosine (C) with guanine (G), have long been considered the key to DNA’s stability, replication, and capacity for information storage, with the hydrogen bonds between them playing an integral role.  Adenine and guanine belong to the double-ringed class of molecules called purines. Cytosine, thymine, and uracil are all pyrimidines. Uracil replaces thymine in RNA. Adenine, guanine, thymine, cytosine and uracil are bases because of the presence of one or more of the following groups: – NH₂, – NH – and = N – groups. Importantly, – NH₂ and – NH – groups can react with carboxylic acids and phosphoric acid to form amides. They are usually simply called bases in genetics. Because A, G, C, and T appear in the DNA, these molecules are called DNA-bases; A, G, C, and U are called RNA-bases. Formation of hydrogen-bonded pairs composed of one purine and one pyrimidine, such as guanine-cytosine and adenine-thymine.

These nucleotides are important for a number of reasons. Most of them, not just ATP, are the sources of energy that drive most of our reactions. ATP is the most commonly used source but GTP is used in protein synthesis as well as a few other reactions. UTP is the source of energy for activating glucose and galactose. CTP is an energy source in lipid metabolism. AMP is part of the structure of some of the coenzymes like NAD and Coenzyme A. And, of course, the nucleotides are part of nucleic acids. Neither the bases nor the nucleotides are required dietary components.

Knowledge of the interaction between biologically active molecules, such as proteins or nucleic acid, and solid surfaces is relevant to the preparation of bio compatible materials and biosensors. The adsorption of small organic molecules, in particular, amino acids or nucleic acid bases, on surfaces is thereby studied to help in the understanding of complex intermolecular processes, e.g., in the origin of life research(25).

Self-organisation of organic molecules appears as one of the most promising approaches to the further miniaturisation of electronic devices. Due to their Watson–Crick complementarity, DNA bases are promising candidates for the design of functional self-organized structures. Two-dimensional structures of self-assembled DNA bases on various substrates, like especially highly oriented graphite or Au (111) surfaces, have been investigated both experimentally and theoretically to a great extent. The thorough understanding of the molecule–substrate interaction is essential for the understanding and successful prediction of the intermolecular interaction of surface adsorbed molecules. In this context, we investigate here computationally the adsorption mechanism of single adenine, guanine, cytosine and thymine molecules on the surface of Boron Nitride (26).

It is of fundamental importance for understanding the function of DNA purine and Pyrimidine bases to understand their spontaneous adsorption on surfaces. For this reason, the theoretical study of nucleic acids and their adsorption on different types of electrode materials has recently been of great interest(27).

Adsorption of small biomolecules on inert surfaces acts as a laboratory of molecular interactions and is an excellent starting point for addressing molecular recognition and self-organization processes. By studying these systems we gain insight into the delicate balance between intermolecular forces that contribute to supramolecular binding, for example, the unique identification of antigens and their binding sites in our biochemistry. It is natural to begin an investigation of molecular interactions and organization by focusing on key building blocks, like the nucleic acids or the amino acids. Three-dimensional biopolymer systems, like the DNA double helix or proteins, permit folding of an extreme complexity that limits direct access to most of the structure, and direct experimental probing of the atomic-scale organization is difficult. Theoretical modeling must therefore map out interactions and organization not only between primary but also secondary and higher order structure in the absence of any calibration with experiments. In contrast, trapping nuclei bases on inert surfaces not only simplifies the possibilities for structural reorganizations but also makes the molecular interactions accessible to direct characterization through advanced atomic-scale experiments(25-27).

The determination of the structure of adsorbed Adenine, Guanine, Cytosine and Thymine on BN surfaces is important for understanding its bonding and reactivity in catalysis and other surface phenomena and adsorption of these molecules on BN may be able to yield changes in the interactions between the BN layer and foreign atoms or molecules (28-31).

In nanostructure research, molecular interaction with the nanostructure surface is a sub field of considerable interest because of potential applications such as storage, chemical sensors, and electronic devices. Doping or functionalizing nanostructures through chemical binding of atoms, molecules, or molecular groups is viewed as a viable approach to tailoring their properties.

We studied the adsorption of Adenine, Guanine, Cytosine and Thymine molecules on the BN sheet by means of density functional theory (DFT) calculations.Adsorption energy ∆Ead (kcal/mol), HOMO- LUMO energy gap ∆Eg (eV), voltage difference ∆V(a.u) and ∆q (e) were studied (32-35).

Computational Methods

The quantum chemical computations in the present work were carried out with Gaussian 2009 software package. The adsorption of the Adenine, Guanine, Cytosine and Thymine molecules was investigated on pristine Boron Nitride using density functional theory calculations.

The geometry of the Boron Nitrid and Adenine, Guanine, Cytosine and Thymine molecules have been optimized by Becke’s hybrid three-parameter exchange functional and the non-local correlation functional of Lee, Yang, and Parr (B3LYP) method with 6-31g* basis set of Barone using ab initio GAUSSIAN quantum chemical package(36-38) . The B3LYP density functional has been previously shown to reproduce experimental proprieties and has been commonly used for nanostructures.

The optimization was done along with a frequency calculation to verify that the geometry was a real minimum without any imaginary frequency. In the current study, we have performed systematic first principle calculations on the atomic and electronic nanostructures. The description of the intra-molecular energy of individual molecules, Boron Nitride and Adenine, Guanine, Cytosine, Thymine is wanted within the nano system as compared with the calculations performed for the free separate molecules. In this approach, we can determine the interaction energy by computing the energy of the free BN and Adenine, Guanine, Cytosine, Thymine individually for every geometrical arrangement of the system. Adsorption energy, energy gap, voltage difference and ∆q have been calculated at the level of Cndo pop=chelp theory.

Resulte and Discussion

In this study, we report adsorption energy (kcal/mol), HOMO energies, LUMO energies and HOMO- LUMO energy gap (eV), voltage difference ∆V, and ∆q calculations for the Boron Nitride layer which are doped by Adenine, Guanine, Cytosine and Thymine molecules in various distances.

The adsorption energy Ead of the Adenine attached BN was calculated as follows:

Ead = E (Adenine/BN) – [ E(BN) + E(Adenine) ]

Where E(Adenine/BN) corresponds to the energy of the Boron Nitride, in which Adenine has been adsorbed on the surface, E(BN) is the energy of the isolated sheet , and E(Adenine) is the energy of a single Adenine molecule.  We calculate other values of adsorption energy for Guanine, Cytosine and Thymine attached BN the same way.

The HOMO-LUMO band gap is a gap between the HOMO (the highest occupied molecular orbital) and LUMO (the lowest unoccupied molecular orbital) (32). In order to check the validity of this description about the structural stability of the Adenine-BN, Guanine-BN, Cytosine-BN and  Thymine-BN  systems, the HOMO–LUMO frontier orbitals have been calculated. Recently, the HOMO–LUMO band gap has been suggested is a measure of the structural stability and semi-conducting properties of. The band gap of these systems as the relative differences in the energy of the HOMO and the LUMO is reported in Tables 1-4. In Figure1 we show the models for adsorption state for molecules on the Boron Nitride.

Figure1: The views of the molecules attached BN. Adenine-BN (a), Guanine-BN (b), Cytosine-BN (c) and Thymine-BN (d) systems.  Click here to View figure

 

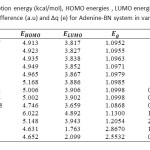Table1: Calculated adsorption energy (kcal/mol), HOMO energies , LUMO energies, HOMO-LUMO energy gap (eV),voltage difference (a.u) and ∆q (e) for Adenine-BN system in various distances  Click here to View table

 

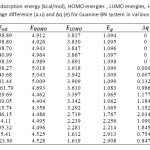Table2: Calculated adsorption energy (kcal/mol), HOMO energies , LUMO energies, HOMO-LUMO energy gap (eV),voltage difference (a.u) and ∆q (e) for Guanine-BN system in various distances  Click here to View table

 

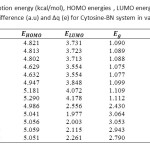Table3: Calculated adsorption energy (kcal/mol), HOMO energies , LUMO energies, HOMO-LUMO energy gap (eV),voltage difference (a.u) and ∆q (e) for Cytosine-BN system in various distances  Click here to View table

 

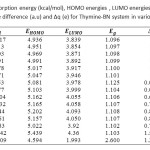Table4: Calculated adsorption energy (kcal/mol), HOMO energies , LUMO energies, HOMO-LUMO energy gap (eV),voltage difference (a.u) and ∆q (e) for Thymine-BN system in various distances  Click here to View table

 

The expectation values of the adsorption energy ∆Ead(kcal/mol), HOMO- LUMO energy gap ∆Eg (eV), voltage difference ∆V(a.u), and ∆q(e) of Adenine-BN, Guanine-BN, Cytosine-BN and Thymine-BN systems are displayed in Figures 2-5 and also these calculated values are compared in Tables 1

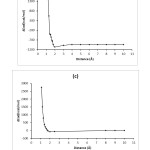Figure2: The graphs of the calculated adsorption energy(kcal/mol) for Adenine-BN (a), Guanine-BN (b), Cytosine-BN (c) and Thymine-BN (d) systems.  Click here to View figure

 

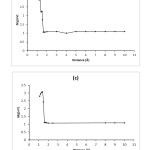Figure3: The graphs of HOMO-LUMO energy gap (eV) for Adenine-BN (a), Guanine-BN (b), Cytosine-BN (c) and Thymine-BN (d) systems.  Click here to View figure

 

Figure4: The graphs of voltage differences (a.u) for Adenine-BN (a), Guanine-BN (b), Cytosine-BN (c) and Thymine-BN (d) systems.  Click here to View figure

 

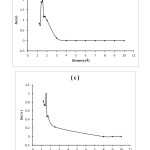Figure5: The graphs of ∆q (e) for Adenine-BN (a), Guanine-BN (b), Cytosine-BN (c) and Thymine-BN (d) systems.  Click here to View figure

 

The Lennard-Jones function is a very famous empirical function in molecular dynamics. The Lennard–Jones potential is an effective potential that describes the interaction between two uncharged molecules or atoms. The Lennard–Jones potential is mildly attractive as two uncharged molecules or atoms approach one another from a distance, but strongly repulsive when they approach too close. As such it is a model for all interatomic pair potentials. Its simplicity and accuracy make it highly suitable for molecular dynamics simulations. The form of the function (V(r)) is given by:

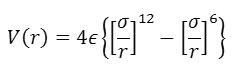
In which r is the interatomic separation, epsilon is the energy constant (or well depth) and sigma is effectively the diameter of one of the atoms.

At short range (small r) the potential energy is large and positive, revealing that this is a very unfavourable arrangement of the atoms (it indicates that the two atoms are strongly overlapping). At long range the potential energy is small and negative. This indicates that at this range the pair of atoms experiences a stabilising influence. (In fact this corresponds to the London dispersion energy, caused by a subtle form of electrical attraction known as the instantaneous dipole-dipole interaction). At a separation slightly greater than sigma, the energy is at a minimum. This where the atom pair is stable, and will be content to remain in this position until some external influence disturbs them. The basic shape of this curve is common to almost all empirical potentials and captures the essentials of interatomic (nonbonding) forces.

We can use the potential energy function to calculate the force between the atoms. Mathematically this is given by the negative of the first derivative of the function – in other words the negative of the slope of the graph at all points. Such a derivation shows that when the atoms are close the force is repulsive, at long range it is attractive, and at the energy minimum, the force is zero – as expected! The mathematical form of the force is as follows:

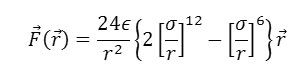
Note that the force F is a vector, with components in three directions: X,Y,Z. This is quite different from the potential function, which is a scalar and has only one value for each distance r. This is one reason why it is more convenient to work with potential functions rather than force laws.

References

1. Monajjemi, M. stru. chem. 2012, 23, 551-580.
2. Monajjemi, M.; Ahmadianarog, M.; Shekari, Z.; Tati, R.; Ilkhani, A. R.; Yamola, H. Fullerenes Nanotubes and Carbon Nanostructures. 2015, 23(3).
3. Monajjemi, M.: Seyedhoseini, M.; Mousavi, M.; Jamali, Z. Fullerenes Nanotubes and Carbon Nanostructures. 2014.
4. Najafpour, J.; Monajjemi, M.; Aghaie, H.; Zare, K. Fullerenes Nanotubes and Carbon Nanostructures. 2015, 23(3).
5. Ardalan, P.; Ardalan, T.; Monajjemi, M.Fullerenes Nanotubes and Carbon Nanostructures. 2014, 22, 687-708.
6. Curl, R. F.; Smalley, R. E. Science. 1988, 242, 1017.
7. Naruhiro, K.; Takeo, O. Solid State Commun. 2004, 131, 121–124.
8. Blase´, X.; Rubio, A.; Louie, S. G.; Cohen, M. L. Europhys Lett. 1994, 28, 335.
9. Miyamoto, Y.; Rubio, A.; Cohen, M. L.; Louie, S. G. Phys. ReV. B 1994, 50, 4976.
10. Chopra, N. G.; Luyken, R. J.; Herrey, K.; Crespi, V. H.; Cohen, M. L.; Louie, S. G.; Zettl, A. Science. 1995, 269, 966.
11. Monajjemi, M. Chem. Phy. 2013, 425, 1-13.
12. Monajjemi, M; Boggs, J. E.  J. Phy. Chem. A. 2013.
13. Monajjemi, M.; Yamola, H.; Mollaamin, F. Fullerenes Nanotubes and Carbon Nanostructures. 2014, 22(6).
14. Mollaamin, F.; Monajjemi, M.; Mehrzad, J. Fullerenes Nanotubes and Carbon Nanostructures. 2014, 22, 738-751.
15. Monajjemi, M.; Kharghanian, L.; Khaleghian, M.; Chegini, H. Fullerenes Nanotubes and Carbon Nanostructures. 2014, 22, 709–725.
16. Petrescu, M. I.; Balint, M. G.  U. P. B. Sci. Bull. 2007, 69, 35-42.
17. Monajjemi, M.; SeyedHosseini, M.;  Molaamin, F. Fullerenes Nanotubes and Carbon Nanostructures. 2013, 21(5).
18. Monajjemi, M.; Jafari Azan, M.; Mollaamin, F. Fullerenes Nanotubes and Carbon Nanostructures. 2013, 21(6).
19. Najafpour, J.; Monajjemi, M.; Aghaie, H.  Journal of Computational and Theoretical Nanoscience 2014, 11(9).
20. Monajjemi, M.; Ahmadianarog, M. Journal of Computational and Theoretical Nanoscience. 2014, 11(6), 1-7.
21. Monajjemi, M.; Wayne Jr. b, R.;  Boggs, J. E. Chem. Phy. 2014, 433, 1–11.
22. Mehrizad, A.; Aghaie, M.; Gharbani, P.; Dastmalchi, S.; Monajjemi, M.; Zare, K. Iranian Journal of Environmental Health Science & Engineering. 2012, 9(1), 5.
23. Monajjemi, M.;Hooshmand, N.; Mollamin, F. International journal of physical sciences. 2011, 6(30), 6899-6909.
24. Mollaamin, F.; Mohajeri, S.; Monajjemi, M. International journal of physical sciences. 2011, 6(16), 3915-3922.
25. Brett, A. M. O.; Da Silva, L. A.; Brett, C. M. A. Langmuir. 2002, 18, 2326-2330.
26. Preuss, M.; Schmidt, W. G.; Bechetedt, F. Physical Review letters. 2005, 94, 236102.
27. Rauls, E.; Blankenburg, S.; Schmidt, W. G. Surface Science. 2008, 602, 2170-2174.
28. Moradi, O.;  Zare, K.; Monajjemi, M.; Yari, M.; Aghaie, H. Fullerenes Nanotubes and Carbon Nanostructures. 2010, 18(3), 285-302.
29. Ghalandari, B.; Monajjemi, M.; Mollaamin, F. Journal of Computational and Theoretical Nanoscience. 2011, 8(7), 1212-1219.
30. Bakhshi, K.;Mollaamin, F.; Monajjemi, M. Journal of Computational and Theoretical Nanoscience. 2011, 8(4), 763-768.
31. Monajjemi, M.; Mollaamin, F. Journal of Cluster Science 2012, 23(2), 259-272.
32. Monajjemi, M.; Lee, V. S.; Khaleghian, M.; Honarparvar, B.; Mollaamin, F. The Journal of Physical Chemistry.2010, 114(36), 15315-15330.
33. Mollaamin, F.; Monajjemi, M. Journal of Computational and Theoretical Nanoscience. 2012, 9(4), 597-601.
34. TazikehLemeski, E.; RezaeiBehbehani, G.; Saboury, A. A.; Monajjemi, M.; ZafarMehrabian, R.; AhmadiGolsefidi, M.; Rajabzadeh, H.; Baei, M. T.; Hasanzadeh, S. Journal of Solution Chemistry. 2011, 40(4), 575-586.
35. Mollaamin, F.; Najafpour, J.; Ghadami, S.; Ilkhani, A. R.; Akrami, M. S.; Monajjemi, M. Journal of Computational and Theoretical Nanoscience.2014.
36. Becke, A. D. J. Chem. Phys. 1993, 98, 5648.
37. Lee, C.; Yang, W.; Parr, R. G. Phys. ReV. B 1998, 37, 785.
38. Golberg, D.; Bando, Y.; Stephan, O.; Kurashima, K. Appl. Phys. Lett. 1998, 73, 2441–2443.

---

This work is licensed under a Creative Commons Attribution 4.0 International License.