Predicting ESR Peaks in the 4d and 5d Transition Metal Ion Complexes by NMR, ESR and NQR Parameters: A DFT Study

Introduction

Only a limited research work had been done in the experimental determination  of  number of ESR peaks  in  complexes of 4d and 5d metal ions [1-5] like  Zr (III) [6-8],Hf (III) [7-9]; Nb (IV) [10-12], Ta (IV) [9]; Tc (II) [9, 13, 14]_, Re (II) [15-17]; Ru (III) [18–24],Os (III) [18-20,24]; Rh (IV) [25-27 ]_,Ir (IV) [26,27]which formed five congeners of 2^nd and 3^rd transition series.

As DFT had, hardly, been applied to determine number of ESR peaks in these metal ion complexes, we tried DFT  implemented in ADF 2010.01 to 34 complexes such as [ZrX₆]^3-(X= F, Cl , Br), [HfX₆]^3- (X=F, Cl, Br), [Hf (NH₃)₆]³⁺, [NbX₆]^2- (X=F, Cl, I, NCS ),  [Nb (NH₃)₆]⁴⁺, [TaX₆]^2-(X=Cl, Br), [TcBr₆]^4-, [Tc (NH₃)₆]²⁺, [ReX₆]^4-(X=Cl, Br), [Re(NH₃)₆]²⁺,[RuX₆]^3-(X=F, Cl , Br), [OsX₆]^3- (X=F, Cl ,Br), [Os (NH₃)₆]³⁺, [RhX₆]^2-  (X=F, Cl, Br), [Rh (NH₃)₆]⁴⁺, [IrX₆]^2-  (X=F, Cl ,Br),  [Ir (NH₃)₆]⁴⁺ belonging   to 10  metal ions of the 2^nd and 3^rd transition series. All these six coordinate complexes containing either weak halo or comparatively stronger (ammine and thiocyanato -N) ligands belonged to five congeners of the 2^nd and 3^rd transition series. They, invariably, possessed one unpaired electron because their large Crystal Field Stabilization Energies (CFSE) would cause pairing of electrons even with the week ligands.

Need of the Study

There were two main reasons which tempted us to take up the present study:

Only a limited research work had been done in the experimental determination of number of ESR peaks in 4d and 5d metal ion complexes because their authentic 10 Dq values were difficult to determine experimentally due to their high values of spin orbit coupling constants (λ_M ⁿ⁺ ) which, in turn, would adversely affect ESR parameters (especially A_ten).

ESR transitions energies falling in microwave region, generally, needed cryogenic conditions which were difficult to obtain and cumbersome to maintain.

Methodology  

ADF (Amsterdam Density Functional) software was installed on Windows XP platform as “ADF jobs”. A new directory was created using “File menu” of ADF jobs. After optimization of the complexes, different commands were filled into the software to obtain ESR, NQR [28-30] and NMR[31-33] parameters which  were discussed in detail  in  our previous publications[28-33].

With to  the specific set of commands, the ADF software would give one ESR {Hyperfine Coupling Constants (A_ten)}, two NQR {Nuclear Quadrupole Coupling Constant (NQCC), Asymmetric Coefficient (η)} [28-30]  and two NMR parameters  {Shielding Constant (σ) , Chemical Shift(δ) }[31-33].These five parameters (A_ten, NQCC,η, σ, δ) together were, then,  used to  predict the number of ESR peaks in the  2^nd and 3^rd transition series metal ion complexes.

Results

Results for 34 complexes of 10 metal ions were tabulated in Tables: 1-2.

Table: 1 contained values of I_M, I_{C A,} g _M and g _CA   as well as μ_M and μ_CA (in terms of b_n  to β_n) and ratios of μ_M and μ_CA to predict the possibility of hyperfine interaction between metal ions and ligands.

Table: 1. Prediction of Hyperfine Interaction between Metals and Ligands Click here to View table

 

Table: 2 contained A_ten, σ, δ values of metal ions and A_ten, NQCC,η, σ, δ and CA of  ligands, number of spatially different ligands along with  the theoretically predicted number of ESR peaks  in these complexes.

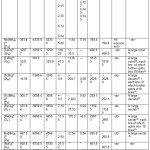Table: 2. Prediction of Number of ESR peaks in Complexes     Click here to View table

 

Discussion  

It was taken up under the following headings

Basis for prediction of number of ESR peaks  

Five parameters (A_ten, NQCC,η, σ, δ ) of metal ions and coordinating atoms (CA) of ligands were obtained from the software by giving it certain commands. A metal ion possessed only one value of each one of these 5 parameters while the values of the parameters might differ in case of the coordinating atoms (CA) of ligands. When, the ligands possessed the same or nearly the same values of these 5 parameters, itindicated that all the ligands were spatially equivalent. The relative magnitudes of the values of the parameters of metal ion and CA would also be taken into account while predicting ESR peaks of the complexes.

Relation  to Calculate of nuclear magnetic moment ((m_M) in terms of b_n:

After knowing the values of nuclear spin quantum numbers and g factors of metals  (I_M, g _M) and of  coordinating atoms (CA) of  ligands (I_CA , g _CA) from the literature, we could calculate nuclear magnetic moments of both the metal (μ_M) and  coordinating atoms (μ_CA) of  ligands in terms of β_n by the following relation:

_μM=g _M [I_M (I_M+1)] ^1/2

and                                                                          (a)

_μCA =g _CA [I_CA (I_CA+1)] ^1/2

Knowing whether hyperfine interaction was possible or not:

From [μ_M/μ_CA] ratio called μ_n ratio, we could draw the following conclusions

A comparable μ_n ratio for isotopes with I >0 having appreciable % natural abundance would mean that the unpaired electron was delocalized both on the metal and the ligands. So the hyperfine interaction between the metal ion and the ligands was most probable.

The peaks would arise both from the ligands and the metal ion

Very small or very large ratios implied that μ_n of ligands and metal differ largely. In such a case, no hyperfine interaction between the metal and the ligands was possible. Electron would remain localized on the metal irrespective of the values of I and the % abundance.

The peaks would arise only from the metal ion

Analogous to an electronic spin: μ_e=g_e [s (s+1)] ^1/2    

Predicting the number of ESR peaks

Assuming I_M andI_CA the nuclear spinsof themetal and [CA] respectively:

Number of ESR peaks given by a metal ion was

2I_M +1                       (b)

Number of ESR peaks arising from ligands was predicted from their spatial

arrangement as follows:

When all the n ligands were spatially equivalent, then each ESR line of metal ion would be split up into the lines:

(2 n I_CA+1)                                 (c)

If n₁ ligands were spatially of one type; n₂ are of the other type and so on, then the total number of lines into which one line of the metal ion would be split:

(2 n₁ I_CA+1)(2n₂ I_CA+1)(2 n₃ I_CA+1)                                            (d)

If all the ligands were nonequivalent, one line of metal ion would split into:

(2 I_CA+1)ⁿ                                                (e)

If metal ion possessed higher A_ten than the coordination atoms (CA) of ligands, we should first calculate number of lines obtained from metal ion. Each line of the metal ion might ,further, split into more number of lines depending upon  whether the ligands could undergo hyperfine with the metal ion or not. Conversely, if the coordinating atoms of ligands had higher A_ten values, then first calculate number of lines from ligands. Each line of ligands should, then, split by metal ion if the hyperfine interaction was possible.

There might occur overlapping of ESR lines from different factors. So experimentally observed number of lines might be less than the theoretically predicted lines. Also, when the predicted number of lines was large and A_ten value/s of species undergoing hyperfine interaction was/were very small, the lines would merge to give a continuum.

The ESR peaks of the following 34 complexes were theoretically predicted.

The metal wise discussion was subdivided into ten headings (5.2-5.11).

Prediction of number of ESR peaks in Zr (III) Complexes

ESR spectra of [ZrX₆]^3- (X=F, Cl, Br) were discussed in two parts

[ZrX₆]^3- (X=F, Br)    

They showed the following features

The six F or Br possessed same values of A _ten, NQCC, η, σ, δ respectively so that all the ligands were  spatially equivalent.

A_ten value of Zr (III) was more than F but lesser than Br.

With small μ_n ratios, the unpaired electron was localized only on Zr(III).

Their ESR spectra gave only a large sextet ^(b) from Z r (III) [2*5/2+1].

[ZrCl₆]^3-    

It showed the following features

As the six Cl had the same A_ten, NQCC,η, σ, δ  values respectively, they should be spatially equivalent.

Unpaired electron was delocalized both on Zr (III) and Cl as their μ_n ratio was comparable [3]. A_ten value of Zr (III)was more than those of the six Cl.

Its ESR spectrum would give a large sextet ^(b) from Zr (III) [2*5/2+1] with each line further splitting into19 lines^(c) by the hyperfine interaction of Zr (III)and six equivalents Cl [2*6*3/2+1].

Prediction of number of ESR peaks in Hf (III) Complexes 

Complexes like [HfX₆]^3- (X=F, Cl, Br) and [Hf (NH₃)₆]³⁺ were studied as follows:

[HfX₆] ^3- (X=F, Br)

They showed the following common features:

The six F or Br were spatially equivalent as they showed the same A_ten, NQCC, η, σ, δ values respectively.

As their μ_n ratios were small, the unpaired electron would remain localized only on Hf (III) with no hyperfine interaction.

A_ten value of Hf (III)was more than those of the F and the Br.

Their ESR spectra should give only an octet ^(b) from Hf (III) [2*7/2+1].

[HfCl₆]^3- and [Hf (NH₃)₆]³⁺

Both showed the following features

The six Cl or NH₃ ligands were spatially equivalent with same A_ten, NQCC, η, σ, δ values respectively.

Unpaired electron was delocalized both on Hf (III)and Cl or NH₃ as their μ_n ratios were comparable.

A_ten of Hf (III) was more than Cl or N of NH₃.

Their spectra showed a large octet^(b) from Hf (III) [2*7/2+1]  with each line further splitting into 19 ^(c)  or13 lines^(c)  by the hyperfine interaction of Hf (III) and the six equivalents Cl [ 2*6*3/2+1] or six N of six NH₃ ligands  [2*6*1+1] respectively.

Prediction of number of ESR peaks in Nb (IV) Complexes

The study included 5 complexes such as: [NbX₆]^2- (X=F, Cl, I, N CS) and [Nb (NH₃)₆]⁴⁺. Their ESR discussion was divided into four parts:

[NbF₆]^2-

It showed the following features:

With the same A_ten, NQCC,η, σ, δ  values  respectively,all the ligands were equivalent.

With comparable μ_n ratio, the unpaired electron was delocalized both on Nb (IV)and the F.

A_ten of Nb (IV) was more than those of the F ligands.

Its spectrum  gave a large decane ^(b) from Nb (IV) [2*9/2+1]with each line splitting into a smaller septet^(c) by the hyperfine interaction of Nb (IV) and the six  F [2*6*1/2+1].

[NbCl₆]^2- and [Nb (NH₃)₆]⁴⁺ 

Both showed the following features:

Six Cl or NH₃ had same values of A_ten, NQCC, η, σ,  δ respectively. So, all the ligands were spatially equivalent respectively.

Unpaired electron was localized on Nb (IV) but not on ligands.

A _ten value of Nb (IV) was more than those of Cl or NH₃.

ESR spectra would give only a large decane ^(b) from Nb (IV) [2*9/2+1] with no hyperfine interaction between Nb (IV) and Cl or NH₃ as their μ_n ratios were large.

[Nb I₆]^2-   

It showed the following features:

There were three sets of A_ten, NQCC,η, σ, δ values respectively  for the iodo ligands; each set having two values. So there were three types of stereo chemically different ligands respectively.

Unpaired electron was delocalized both on Nb (IV) and ligands as μ_n ratio of Nb and I was comparable respectively.

A_ten value of Nb (IV) was more than those of the iodo ligands respectively.

Its spectrum  showed a large decane ^(b) from Nb (IV) [2*9/2+1] with each line splitting into 1331 lines [2*2*5/2+1]³ from  hyperfine  interaction between Nb (IV) and the six iodo  ligands. In fact, its ESR spectrum would exhibit a continuum.

[Nb (NCS) ₆]^2- 

It showed thefollowing features

There were three sets of A_ten, NQCC,η, σ, δ values respectively  for the  isothiocyanato ligands; each set having two values. So there were three types of stereo chemically different ligands.

Unpaired electron was localized on Nb (IV) as μ_n ratio of Nb and N of NCS^1-was small.

A_ten value of Nb (IV) was more than N of ligands.

Its spectrum should give only a large decane ^(b) from Nb (IV) [2*9/2+1] with no

hyperfine interaction between Nb (IV) and the six  isothiocyanato   ligands.

Prediction of number of ESR peaks in Ta (IV) Complexes

Two complexes such as [Ta X₆]^2- (X= Cl, Br) were studied

[Ta Cl₆]^2- 

It showed the following features

Six chloro ligands were equivalent as they possessed the same A_ten, NQCC, σ, δ values respectively.

As their μ_n ratio was small, the unpaired electron remained localized only on Ta (IV) with no hyperfine interaction.

A_ten of Ta (IV) was more than those of six equivalent chloro ligands.

So its ESR spectrum would give a large octet ^(b) from Ta (IV) [2*7/2+1] only.

[TaBr₆]^2-

It showed the following features

Six bromo ligands were equivalent with same A _ten, NQCC, σ, δ values respectively.

With comparable μ_n ratio, the unpaired electron was delocalized both on ligands and Ta (IV).

A _ten of Ta (IV) was more than the bromo ligands.

Thus its spectrum  would give a large octet ^(b) from Ta (IV) [2*7/2+1] whose each line split into 19 lines^(c) by the hyperfine interaction between Ta(IV) and six equivalents Br [2*6(3/2+1].

Prediction of number of ESR peaks in Tc (II) Complexes

The complexes like [Tc Br₆]^4-and [Tc (NH₃)₆]²⁺ were studied.

[TcBr₆]^4-

It showed the following features:

With same A _ten, NQCC,η, σ, δ values  respectively, the six bromo ligands  were equivalent.

With comparable μ_n ratio, unpaired electron was delocalized both on Tc (II)and Br ligands.

A_ten of Tc (II) was more than the Br ligands.

Its spectrum showed a large decane ^(b) from Tc (II) [2*9/2+1].Each line of this  decane would, further, split into smaller 19lines^(c) due to hyperfine interaction between Tc (II) and six stereo chemically equivalent bromo ligands [2*6*3/2+1].

[Tc (NH₃)₆]²⁺

It showed the following features:

With the same A_ten, NQCC, η, σ, δ values  respectively,  six NH₃ ligands were equivalent.

As their m_n ratio was large, the unpaired electron was localized on Tc (II)only.

A_ten value of Tc (II) was less than those of N of NH₃ ligands.

Its ESR spectrum would give only a large decane ^(b) from Tc (II) [2*9/2+1] with no hyperfine splitting between Tc (II)  and  NH₃ ligands as their μ_n ratio was large.

Prediction of number of ESR peaks in Re (II) Complexes

It included three complexes such as: [Re X₆]^4- (X=Cl, Br) and [Re (NH₃)₆]²⁺.

[Re Cl₆]^4- and [Re (NH₃)₆]²⁺

Both showed the following features:

With the same A_ten, NQCC,η, σ, δ values respectively, the six  Cl  and the NH₃ ligands were equivalent.

Unpaired electron was localized only on Re (II) as there was no hyperfine interaction between Re (II) and ligands due to large η_n ratios respectively.

A _ten of Re (II) was more than those of Cl or N of NH₃.

Their ESR spectra showed only a large sextet ^(b) from Re (II) [2*5/2+1].

[Re Br₆]^4-

It showed the following features:

With the same A_ten, NQCC, η, σ, δ values  respectively, the six bromo ligands were equivalent.

Unpaired electron was delocalized both on Re (II) and stereo chemically equivalent bromo ligands as their μ_n ratio was comparable.

A _ten of Re (II) was more than those of bromo ligands.

Its ESR spectrum would show a large sextet ^(b) from Re (II) [2*5/2+1]. Each line of this  sextet, further, split up into a smaller 19 line^(c) pattern due to hyperfine interaction between Re (II) and six equivalents Br [2*6*3/2+1].

Prediction of number of ESR peaks in Ru (III) Complexes

Three complexes such as [RuX₆]^3- (X= F, Cl, Br) were included.

[RuF₆]^3-(X=F, Br)

They showed the following features:

With the same A _ten, NQCC, η, σ, δ values respectively, all the ligands were equivalent.

The unpaired electron was present only on Ru (III) because with small μ_n ratios, there was no hyperfine interaction between Ru (III) and F or Br.

A_ten of Ru (III)was more than the F or the Br.

Their ESR spectra gave only large sextet ^(b) from Ru (III) [2*5/2+1].

[RuCl₆]^3-

It showed the following features:

With the same A_ten, NQCC,η, σ, δ values respectively,  the six Cl  were equivalent.

With comparable μ_n ratio, the unpaired electron was delocalized both on Ru (III) and six Cl.

A_ten of Ru (III)was more than those of the ligands.

Its ESR spectrum showed a large sextet ^(b) from Ru (III) [2*5/2+1] with each line of which would, further, split into smaller 19 lines ^(c) by the hyperfine interaction of six Cl [2*6*3/2+1] and Ru (III).

Prediction of number of ESR peaks in Os (III) Complexes

It included four complexes such as [Os X₆]^3- (X= F, Cl, Br) and [Os (NH₃)₆]³⁺  

[OsX₆]^3- (X=F, Br)

Both the complexes showed the following common features:

With same A_ten, NQCC,η, σ, δ values, all the ligands were equivalent.

Unpaired electron was localized on Os (III).

A_ten of Os (III) was more than the F or the Br.

Their ESR spectra gave a large quartet ^(b) from Os (III) [2*3/2+1] as there was no hyperfine interaction between Os (III) and the F or the Br due to small μ_n ratio.

[OsCl₆]^3-

It showed the following features:

With same A_ten, NQCC,η, σ, δ values  respectively, the six Cl were equivalent.

The unpaired electron was delocalized on both Os (III) and the six equivalents Cl.

The A _ten value of Os (III) was more than those of the six Cl.

Its ESR spectrum showed  a large quartet ^(b) from Os (III) [2*3/2+1].Each line of this quartet further split up into 19 lines^(c) from six spatially equivalents Cl  [2*6*3/2+1] due to hyperfine interaction as their m_n ratio was comparable.

[Os (NH₃)₆]³⁺

It showed the following features

There were three sets of A_ten, NQCC,η, σ, δ values respectively  for the  six N of the six NH₃ ; each set having two values.  So there were present three types of stereo chemically different ligands respectively.

Unpaired electron was delocalized both on Os (III) and the six NH₃ as μ_n ratio of Os and Nwas comparable.

A _ten value of Os (III) was more than those of the ligands

Its spectrum would give a large quartet ^(b) from Os (III) [2*3/2+1] whose each line would, further, split into 125^(d) lines[2*2*1+1]³  from 3 types of stereochemically different  NH₃ by the hyperfine interaction between Os(III) and the  ligands. In fact, its ESR spectrum would exhibit a continuum.

Prediction of number of ESR peaks in Rh (IV) Complexes

It included four complexes: [RhX₆]^2- (X= F, Cl, Br) and [Rh (NH₃)₆]⁴⁺ which showed the following features:

With the same A_ten, NQCC, η, σ, δ values  respectively, the ligands like F, Cl, Br, NH₃  were equivalent.

The unpaired electron was present only on Rh (IV).   

A_ten of Rh (IV) was more  than  the F, Cl or Br or N of  NH₃.

Their ESR spectra should give only a large doublet ^(b) from Rh (IV)[2*1/2+1] with no hyperfine interaction between Rh (IV)and any one of the four different types of ligands due to small μ_n ratios between Rh (IV) and the ligands respectively.

Prediction of number of ESR peaks in Ir (IV) Complexes

It included four complexes: [IrX₆]^2- (X= F, Cl, Br) and [Ir (NH₃)₆]⁴⁺ which showed the following features:

With the same A_ten, NQCC, η, σ, δ values  respectively, the ligands like F, Cl, Br, NH₃  were equivalent.

The unpaired electron was present only on Ir (IV)   (3) A _ten of Ir (IV) was more  than  the F, Cl or Br or N of  NH₃.

Their ESR spectra would give only a large quartet ^(b) from Ir (IV) [2*3/2+1] because no hyperfine interaction between Ir (IV)and any one of four different types of  ligands  due to  small μ_n ratios between Ir(IV) and ligands respectively.

Conclusion

Simply by knowing I and g_n of metals and coordinating atoms (CA) of the ligands from the literature; calculating their nuclear magnetic moments and thus their relative μ_n  ratios, we could  predict the number or ESR lines  in  a vast number of complexes of 10 metal ions of  2^nd and 3^rd transition series which, hitherto, seemed  tenacious   experimentally.. In addition, there lies  a  future use of this study in predicting the number of ESR peaks in complexes containing a very large  variety of spatially different NMR and ESR active both quadrupolar and nonquadrupolar coordinating nuclei because the software allows us to select or ignore the interacting nuclei at our choice. This clearly makes the DFT a very powerful diagnostic tool at the hands of the theoretical Chemists to deduce the future applications of transition metal complexes.

Acknowledgements          

Authors gratefully acknowledge the kind and willing cooperation of Mr. Sunil Chawla [sunil@seascapelearning.com] of ADF (http://www.scm.com).They feel indebted to Mr. S.R. Heer, Chief Engineer (Retd.), North Zone, Doordarshan, New Delhi (India) for his invaluable cooperation in the installation and smooth working of the ADF software.

References

1. Orio, M.; Pentazis, M. D.; Neese, A. F. Photosynthesis Res. 2009, 102, 443-53.
   CrossRef
2. Autschbach, J., Zheng, S.; Schurko, R. W.  Concepts in Magnetic Resonance, Part A. 2010, 36 A, 84–126
3.  Saladino, A. C.; Larsen, S. C. Catalysis Today. 2005, 105, 122–33.
   CrossRef
4.  Pantazis, D. A.; Chen, X. Y.; Landis, C. F.; Neese, F. J. Chem. Theory Comput. 2008, 4, 908–19.
   CrossRef
5. Fritscher, J.; Hrobárik, P.; Kaupp, M. J. Phys. Chem. B. 2007, 111, 4616-29.
   CrossRef
6. Yang, S. Y.; Ziegler, T. Organometallics. 2006, 25, 887-900.
   CrossRef
7.  Fischer, H. Inorganic Radicals, Metal Complexes and Nonconjugated Carbon Centered Radicals. Part 2.26 A, 2006, 1-6.
8.  Kaim, W.; Schwederski, B. Landolt-Borstein- GroupII Molecules and Radicals  pp 1-63 Radicals in metal complexes. Ch- 3.5: Vol. 26A2.
9.  Irikura, K. K.; Goddard, W. A. J. Amer. Chem. Soc. 1994, 116, 8733–40.
   CrossRef
10. Oltmanns, P.; Rehder, D.  J.  Org. Chem. 1988, 345, 87-96.
    CrossRef
11. Wong, E. W.; Walsby, C. J.; Storr. T.; Leznoff, D. B. Inorg. Chem. 2010, 49, 3343-50.
    CrossRef
12.  Patchkovskii, S.; Ziegler, T.  J. Am. Chem. Soc. 2000, 122, 3506–16.
    CrossRef
13.  Yoshimura, T.; Ikai, T.; Takayama, T.; Sekine, T.; Kino, Y.; Shinohara, A.  Inorg. Chem. 2010, 49, 5876-88.
    CrossRef
14. Kudo, T.; Tsuchihashi, N.; Ogata, T.  Radioanalytical and Nuc. Chem. 1987, 118, 169-75.
    CrossRef
15.  Kozlova, S. G.; Gabuda, S. P.; Brylev, K. A.; Mironov,Y. V.; Fedorov, V. E.   J. Phys. Chem. 2004, 108, 10565 –67.
    CrossRef
16. Gancheff, J. S.; Denis, P. A. Phys. Chem. A. 2011, 115, 211-18.
    CrossRef
17. Pacheco, M.; Cuevas, A.; González-Platas, J.; Faccio, R.; Lloret, F.; Julve, M.;  Kremer, C. Dalton Trans. 2013, 42, 15361-71.
    CrossRef
18. Esteves, M. C.; Vugman, N. V.; Leitão, A. A.; Bielschowsky, C. E. J. Phys. Chem. A. 2007, 111, 7218–22.
    CrossRef
19. Liao, M. S.; Scheiner, S. Chem. Phys., 2002, 285, 195-206.
    CrossRef
20. Baraldo, L. D.; Olabe, L. M. Inorg. Chem., 2001, 40, 5704 –07.
    CrossRef
21.  Vrieze, K.; Koten. G. V. Inorg.  Chim. Acta. 1985, 100, 79-96.
    CrossRef
22. Gancheff, J. S.; Denis, P. A.; Drescher, M.; Rainer, W. F.; Rigaut, S. Organometallics, 2010,  29, 5912-18.
    CrossRef
23. Kowalski, K.; Rainer, M. L.; Winter, F.; Zabel, M.; Zalis, S.; Kelm, H.; Kroger, H. J.; Sarkar, B; Kaim, W. Organometallics, 2009, 14, 4196-4209.
    CrossRef
24. Sakaki, S.; Yanase, Y.; Hagiwara, N.; Takeshita, T.; Naganuma, H.; Ohyoshi, A.; Ohkubo, K. J. Phys. Chem., 1982, 86, 1038–43.
    CrossRef
25.  Seuret, P.; Cicoira, F.; Ohta, T.; Doppelt, P.; Hoffmann, P.; Weber, J.; Wesolowski, T. A. Phys. Chem., 2003, 5, 268–74.
26. Tsung, W.Thesis,:Thesis,“Tris(guanidinato)complexes of iridium and rhodium in the oxidation states +III and +IV: synthesis, characterization, and reactivity,”  University of Iowa . 2011.
27. Adams, C. J.; Anderson, K. M.; Charmant, J. P.; Connelly, N. G.; Field, B. A.;
28. Hallett, A. J.; Horne, M. Dalton Trans. 2008, 28, 2680-92.
29. Singh, H.; Bhardwaj, A. K.; Sehgal, M. L.; Mittal, S. K. Int. J. Current Res. Rev. 2012, 4,   12-28.
30. Singh, H.; Bhardwaj, A. K.; Sehgal, M. L.; Mittal, S. K. Int. J. Current Res. Rev. 2013, 5, 13-31.
31. Singh, H.; Bhardwaj, A. K.; Sehgal, M. L.; Mittal, S. K. Int. J. Current Res. Rev 2013, 5, 71- 88.
32. Sharma, S.; Chander, S.; Sehgal, M. L.; Ahmad, I.  Oriental J.Chem. 2015, 31, 1417-27.
    CrossRef
33. Singh, H.; Bhardwaj, A. K.; Sehgal, M. L.; Ahmad, I. Oriental J.Chem.2015, 31, 671-79.
    CrossRef
34. Singh, H.; Bhardwaj, A. K.; Sehgal, M. L.; Javed, M.; Ahmad, I. Oriental J.Chem. 2015, 31, 1461-68.
    CrossRef

---

This work is licensed under a Creative Commons Attribution 4.0 International License.